论文理解【Offline RL】—— A dataset perspective on offline reinforcement learning
- 标题:A dataset perspective on offline reinforcement learning
- 标题(初版):Understanding the Effects of Dataset Characteristics on Offline Reinforcement Learning
- 文章链接:A dataset perspective on offline reinforcement learning
- 发表:NIPS 2021 Workshop on Ecological Theory of RL
- 领域:离线强化学习(offline/batch RL)—— 数据集分析
- 摘要:由于训练过程中策略是次优的,直接在现实世界环境中应用强化学习(RL)是昂贵且有风险的。Offline RL 通过禁止与环境交互避免了此问题。这种情况下,策略是从给定的数据集中学习的,因此数据集唯一地决定了策略性能。一个难题是,研究数据集特征如何影响 Offline RL 算法。注意到数据集的特征是由采样该数据集的 behavior policy 决定的。因此,我们将 behavior policy 的特征定义为 “探索性”:在与 MDP 的交互中产生高信息期望(high expected information);和 “利用性”:具有高期望回报。我们在确定性 MDPs 下,对通过 behavior policy 采样的数据集实现了上述两个指标的经验度量empirical measure。经验度量 SACo 是由归一化的不同 ( s , a ) (s,a) (s,a) pair 数量定义的,代表探索性;经验测量 TQ 是由归一化平均轨迹 return 定义的,代表利用性能。大规模实验证明了 TQ 和 SACo 的有效性,我们发现:无约束的 off-policy DQN 系列方法需要具有高SACo 的数据集来找到一个好的策略;策略约束算法在具有高 TQ 和高 SACo 的数据集上表现良好;对于具有高 TQ 的数据集,纯数据集约束的行为克隆方法与最好的 Offline RL 算法是可比的
文章目录
- 1. 背景
- 1.1 Offline RL
- 1.2 离线数据集
- 2. 本文方法
- 2.1 数据集特征指标
- 2.1.1 探索性指标:transition熵
- 2.1.2 利用性指标:期望轨迹return
- 2.2 抽象MDP(AMDP)
- 2.2.1 定义和理解
- 2.2.2 利用 AMDP 说明两个指标的稳定性
- 2.3 指标实用化
- 2.3.1 探索性指标:SACo
- 2.3.2 利用性指标:TQ
- 3. 实验
- 3.1 生成数据集的方法
- 3.2 实验结果
- 3.2.1 数据集特征对比
- 3.2.2 数据集特征对 Offline RL 算法的影响
- 4. 总结
1. 背景
1.1 Offline RL
Offline RL是这样一种问题设定:Learner 可以获取由一批 episodes 或 transitions 构成的固定交互数据集,要求 Learner 直接利用它训练得到一个好的策略,而且禁止 Learner 和环境进行任何交互,示意图如下
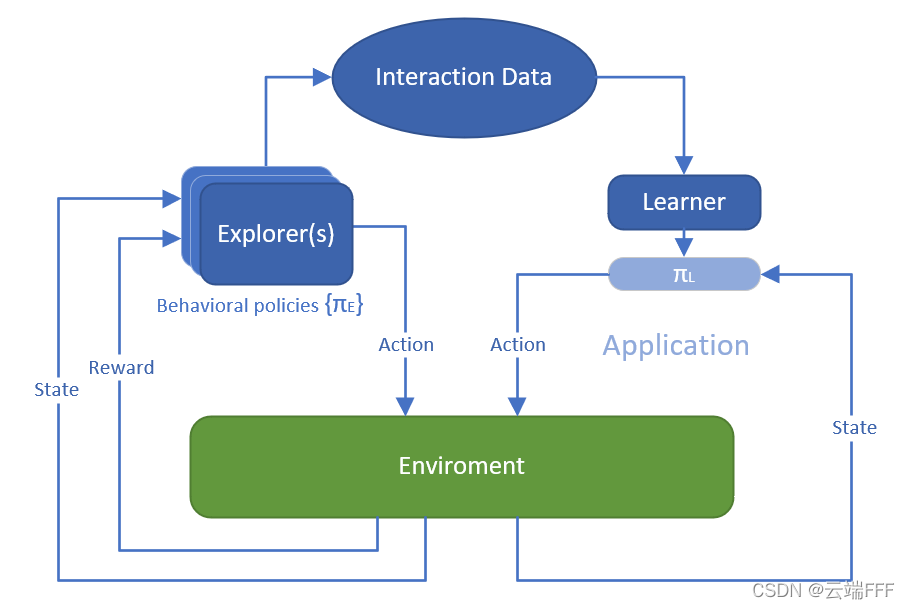
- 关于 Offline RL 的详细介绍,请参考 Offline/Batch RL简介
1.2 离线数据集
-
注意到 Offline-RL 其实和监督学习类似,都是利用一个 fixed 数据集进行学习,但由于特殊的问题设定,Offline-RL 数据集的构成方式特别自由,大部分论文都使用了自己特殊的构造方式。最常见的做法是从零开始训练一个 Online RL agent 至收敛,然后用整个训练过程上的所有交互数据组成数据集, BAIL 这篇文章揭示了这种方案的一个问题:如果使用不同的随机种子,即使是完全相同的 Online RL agent,用其得到的 Offline 数据集做 Offline RL,都有可能得到截然不同的结果
One important observation we make, which was not brought to light in previous batch DRL papers, is that batches generated with different seeds but with otherwise exactly the same algorithm can give drastically different results for batch DRL.
-
作者想要研究离线数据集特征对 Offline-RL 算法性能的影响。注意到数据集对 RL agent 性能的影响主要体现在
分布漂移distribution shift问题上(即 Online 性能测试时 agent 遇到的 ( s , a ) (s,a) (s,a) 分布与训练时面对的 Offline Dataset 不同,策略无法良好地泛化到未见 ( s , a ) (s,a) (s,a) 处),而分布漂移由以下两个因素导致- Online 测试时,agent 和环境交互的非平稳性质
- Offline 数据集的构造过程
固定 Offline RL 算法时,因素 1 中学得的 agent 策略也仅由数据集决定,因此导致分布漂移的核心因素就是使用行为策略构造离线数据集的过程,下图可视化了不同 behavior policy 生成的 offline dataset ,行为策略对数据集的影响肉眼可见
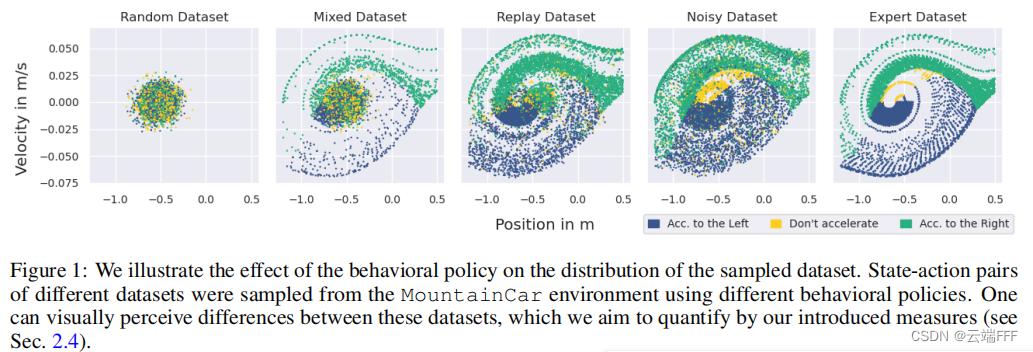
-
综合上述分析,生成离线数据集时使用的 “行为策略的特征” 就可以看做 “离线数据集特征”,作者通过数据集分析得到关于 behavior policy 特征的两个指标,用做离线数据集的特征指标,借以考察离线数据集对 Offline RL 算法的影响,如下所示
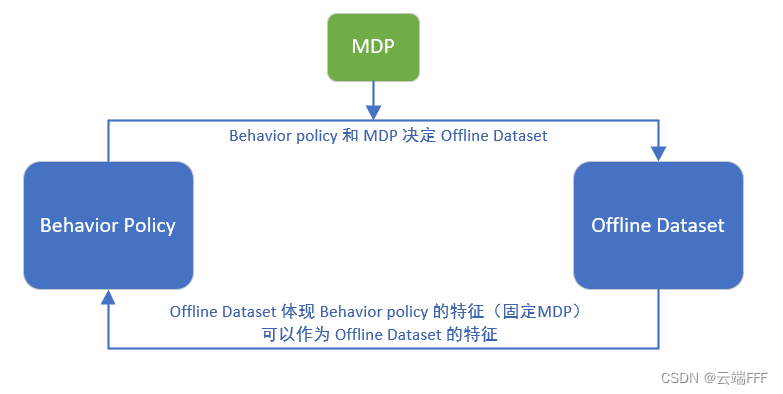
2. 本文方法
- 这篇文章主要是一个分析性质的文章,没有提什么方法,概括一下本文的贡献
- 提出了能够刻画 Offline Dataset 特征的两个实用指标(empirical measure)
- 用覆盖过去论文的多种方式构造 Offline Dataset,借助提出的指标观察由于构造方法不同所导致的数据集特征差异
- 使用构造的数据集对多种 Offline RL 算法进行测试,考察离线数据集特征对学得策略性能的影响
2.1 数据集特征指标
2.1.1 探索性指标:transition熵
-
策略和环境交互的过程可以看成一个单一的生成 transition ( s , a , r , s ′ ) (s,a,r,s') (s,a,r,s′) 的随机过程,如果一个 behavior policy 有高概率可以产生很多不同的 transition,就可以认为该策略具有
探索性explorativenessNote:由于 transition 是通过和给定 MDP 的交互过程产生的,所以策略的探索性只能和 MDP 一起定义。在一个 MDP 中很有探索性的策略可能在另一个 MDP 中缺乏探索性。比如一个带门的迷宫环境,如果门都是打开的,一个随机移动策略可能就有不错的探索性;如果门都是关闭的,随机移动策略由于不会开门,agent 只能卡在一个房间中
-
上述指标可以实现为 transition 的香农熵
H ( p π ( s , a , r , s ′ ) ) : = − ∑ s , a , r , s ′ p π ( s , a , r , s ′ ) > 0 p π ( s , a , r , s ′ ) log ( p π ( s , a , r , s ′ ) ) 、 (1) H\left(p_{\pi}\left(s, a, r, s^{\prime}\right)\right):=-\sum_{\substack{s, a, r, s^{\prime} \\ p_{\pi}\left(s, a, r, s^{\prime}\right)>0}} p_{\pi}\left(s, a, r, s^{\prime}\right) \log \left(p_{\pi}\left(s, a, r, s^{\prime}\right)\right)、 \tag{1} H(pπ(s,a,r,s′)):=−s,a,r,s′pπ(s,a,r,s′)>0∑pπ(s,a,r,s′)log(pπ(s,a,r,s′))、(1) 其中 transition 分布概率 p ( s , a , r , s ′ ) p\left(s, a, r, s^{\prime}\right) p(s,a,r,s′) 可以分解
p ( s , a , r , s ′ ) = p ( s ′ , r ∣ s , a ) p ( s , a ) p\left(s, a, r, s^{\prime}\right)=p\left(s^{\prime}, r \mid s, a\right) p(s, a) p(s,a,r,s′)=p(s′,r∣s,a)p(s,a) 其中 p ( s ′ , r ∣ s , a ) p\left(s^{\prime}, r |s, a\right) p(s′,r∣s,a) 是 MDP 的状态转移矩阵, p ( s , a ) p(s,a) p(s,a) 是行为策略 π \pi π 诱导的 ( s , a ) (s,a) (s,a) 分布,可以替换为(不折扣的)占用度量 ρ π ( s , a ) \rho_\pi(s,a) ρπ(s,a)。利用这个关系可以把等式(1)进一步分解为
H ( p π ( s , a , r , s ′ ) ) = ∑ s , a ρ π ( s , a ) H ( p ( r , s ′ ∣ s , a ) ) + H ( ρ π ( s , a ) ) (2) H\left(p_{\pi}\left(s, a, r, s^{\prime}\right)\right)=\sum_{s, a} \rho_{\pi}(s, a) H\left(p\left(r, s^{\prime} \mid s, a\right)\right)+H\left(\rho_{\pi}(s, a)\right) \tag{2} H(pπ(s,a,r,s′))=s,a∑ρπ(s,a)H(p(r,s′∣s,a))+H(ρπ(s,a))(2) 附证明过程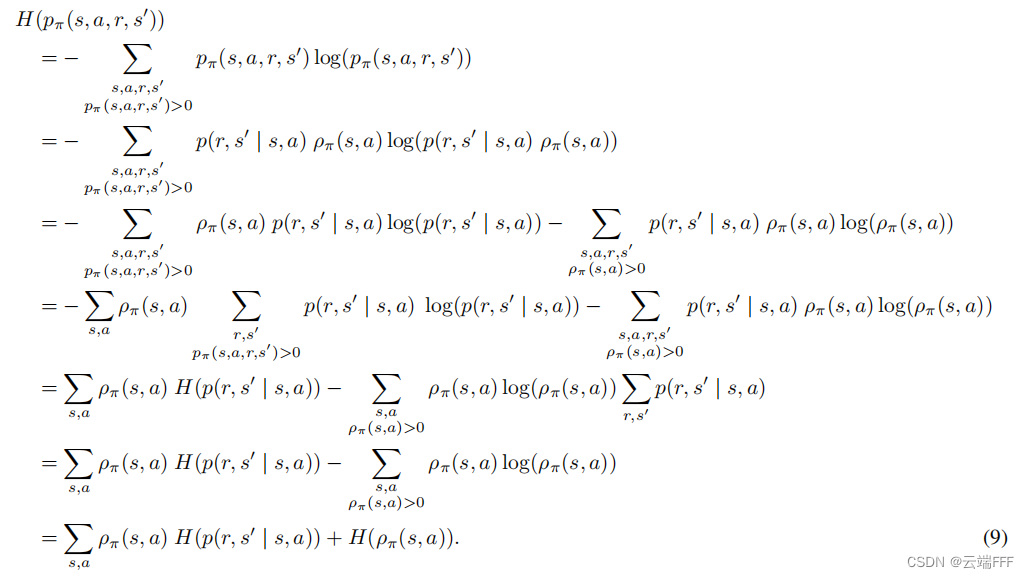
分析等式(2)的成分
- 状态转移矩阵 p ( s ′ , r ∣ s , a ) p\left(s^{\prime}, r |s, a\right) p(s′,r∣s,a) 仅由 MDP 决定
- 占用度量 ρ π ( s , a ) \rho_\pi(s,a) ρπ(s,a) 由策略 π \pi π 和 MDP 共同决定的,因为 ρ π ( s , a ) = p π ( a ∣ s ) p π ( s ) \rho_\pi(s,a) = p_\pi(a|s)p_\pi(s) ρπ(s,a)=pπ(a∣s)pπ(s),而 p π ( s ) p_\pi(s) pπ(s) 可以借助转移概率 p ( s ′ ∣ s , a ) p(s'|s,a) p(s′∣s,a) 递归定义为 p π ( s ′ ) = ∑ s p π ( s ) ∑ a p π ( a ∣ s ) p ( s ′ ∣ s , a ) p_\pi(s')=\sum_sp_\pi(s)\sum_ap_\pi(a|s)p(s'|s,a) pπ(s′)=∑spπ(s)∑apπ(a∣s)p(s′∣s,a)
直观地看,等式 (2) 说明一个高探索性的策略,需要在 “等概率访问所有 ( s , a ) (s,a) (s,a)” 和 “更多访问状态转移随机性 p ( r , s ′ ∣ s , a ) p(r,s'|s,a) p(r,s′∣s,a) 高的 ( s , a ) (s,a) (s,a) 之间进行权衡”。总之,我们得到评估确定性 MDP 问题离线数据集探索性(生成数据集的 behavior policy 探索性)的合理指标为:
transition的熵 -
本文作者只考虑确定性 MDP,也就是说每个 ( s , a ) (s,a) (s,a) 访问后转移到的 ( s ′ , r ) (s',r) (s′,r) 都是确定性的,这时 H ( p ( r , s ′ ∣ s , a ) ) = 0 H\left(p\left(r, s^{\prime} \mid s, a\right)\right)=0 H(p(r,s′∣s,a))=0,等式 (2) 可以进一步化简为占用度量的熵
H ( ρ π ( s , a ) ) : = − ∑ s , a ρ π ( s , a ) > 0 ρ π ( s , a ) log ( ρ π ( s , a ) ) (3) H\left(\rho_{\pi}(s, a)\right):=-\sum_{\substack{s, a \\ \rho_{\pi}(s, a)>0}} \rho_{\pi}(s, a) \log \left(\rho_{\pi}(s, a)\right) \tag{3} H(ρπ(s,a)):=−s,aρπ(s,a)>0∑ρπ(s,a)log(ρπ(s,a))(3) 在一个简单的迷宫问题上使用占用度量熵指标考察随机策略和引入 ϵ \epsilon ϵ 随机的专家策略,可以看到显著区别
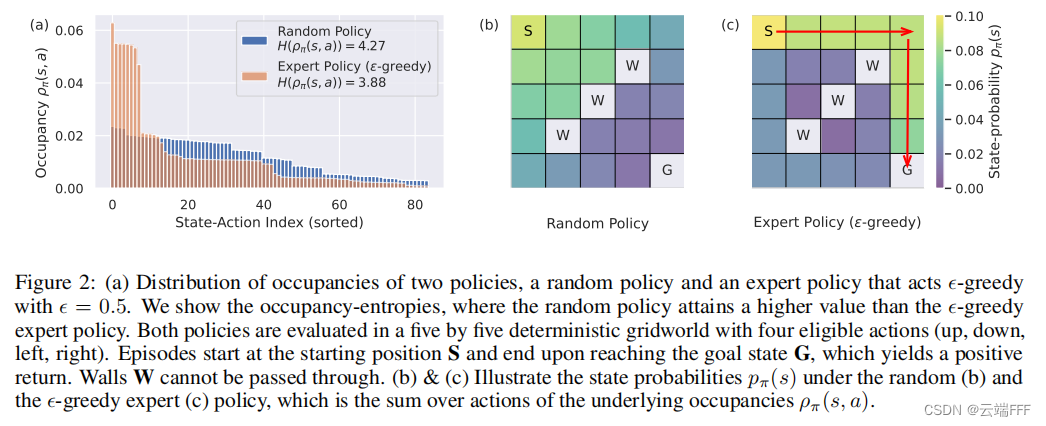
这说明了transition的熵这个指标在确定性 MDP 环境中的有效性
2.1.2 利用性指标:期望轨迹return
- 这个就是 RL 的一般思路,如果离线数据集中高 return 的轨迹越多,说明生成数据集的 behavior policy 有更高概率是一个较好的策略,这些策略对于环境知识的 “利用” 程度更高,最典型的例子就是专家策略
- 因此,评估确定性 MDP 问题离线数据集利用性(生成数据集的 behavior policy 利用性)的合理指标为:
期望轨迹return
g T : = E τ ∼ T [ ∑ t = 0 ∞ γ t r t ∣ r t ∈ τ ] (4) g_\mathcal{T} := \mathbb{E}_{\tau\sim\mathcal{T}}\left[\sum_{t=0}^\infin\gamma^tr_t|r_t\in\tau\right] \tag{4} gT:=Eτ∼T[t=0∑∞γtrt∣rt∈τ](4) 其中 T \mathcal{T} T 是数据集中轨迹的分布, τ \tau τ 代表一条轨迹 - 注意,这个指标对于 D4RL论文 中提到的 behavior policy 为 “Non-representable behavior policies”、“non-Markovian behavior policies” 等情况也适用,简单说就是它可以评估那些我们不能表示数据集生成行为,但可以无限地生成数据的策略(比如人类行为生成的数据集)
2.2 抽象MDP(AMDP)
- 注意到作者提出的两个指标都是和 MDP 相关的,作者希望这些指标关于 MDP 有 “稳定性”。就是说,如果 MDP 的 “状态空间”、“动作空间” 或 “转移矩阵” 有轻微修改,两个指标的值也应该发生小变化,而不是发生突变
2.2.1 定义和理解
-
为了形式化描述 MDP 的(微小)变化,作者借用了之前工作提出的
抽象MDP(AMDP)的概念,定义如下

这个定义简单说就是给定两个 MDP M = ( S , A , R , p , γ ) M=(\mathcal{S,A,R},p,\gamma) M=(S,A,R,p,γ), M ~ = ( S ~ , A ~ , R ~ , p ~ , γ ) \tilde{M}=(\tilde{\mathcal{S}},\tilde{\mathcal{A}},\tilde{\mathcal{R}},\tilde{p},\gamma) M~=(S~,A~,R~,p~,γ) 以及两个 MDP 上的策略 π \pi π 和 π ~ \tilde{\pi} π~- 动作空间 S , S ~ \mathcal{S},\tilde{\mathcal{S}} S,S~ 和状态空间 A , A ~ \mathcal{A},\tilde{\mathcal{A}} A,A~ 都能被某些满射的抽象函数映射到一个公共的 AMDP ( S ^ , A ^ , R ^ , p ^ , γ ) (\hat{\mathcal{S}},\hat{\mathcal{A}},\hat{\mathcal{R}},\hat{p},\gamma) (S^,A^,R^,p^,γ) 的状态空间 S ^ \hat{\mathcal{S}} S^ 和动作空间 A ^ \hat{\mathcal{A}} A^ 上
- 如果 π , π ~ \pi,\tilde{\pi} π,π~ 经过对应的映射后会得到相同的抽象策略 π ^ \hat{\pi} π^,则他们诱导的轨迹分布 T , T ~ \mathcal{T},\tilde{\mathcal{T}} T,T~ 也有相同的抽象分布 T ^ \hat{\mathcal{T}} T^
下图给出两个简单例子

-
下面给出更多例子,方便理解 AMDP 的定义和特性
- 利用 AMDP 屏蔽表示形式的差异
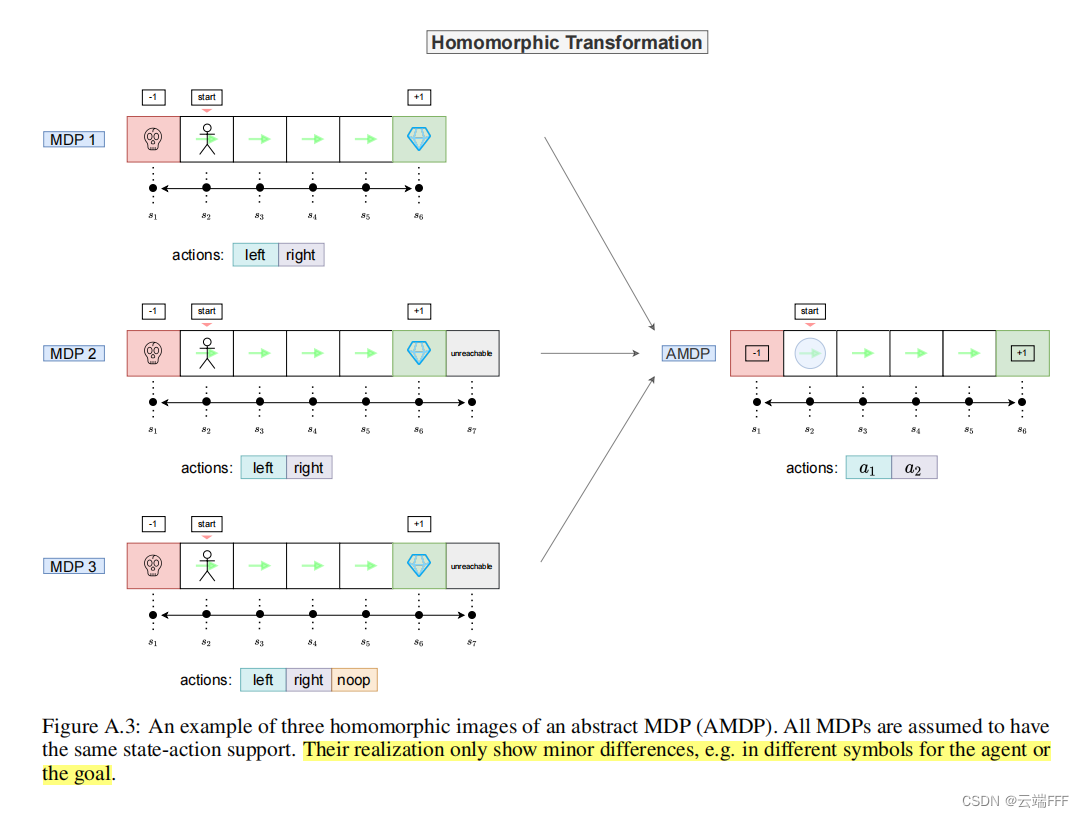
- 如果不同的具体 MDP 具有同态的可行轨迹(策略),它会在 AMDP 中被保留下来
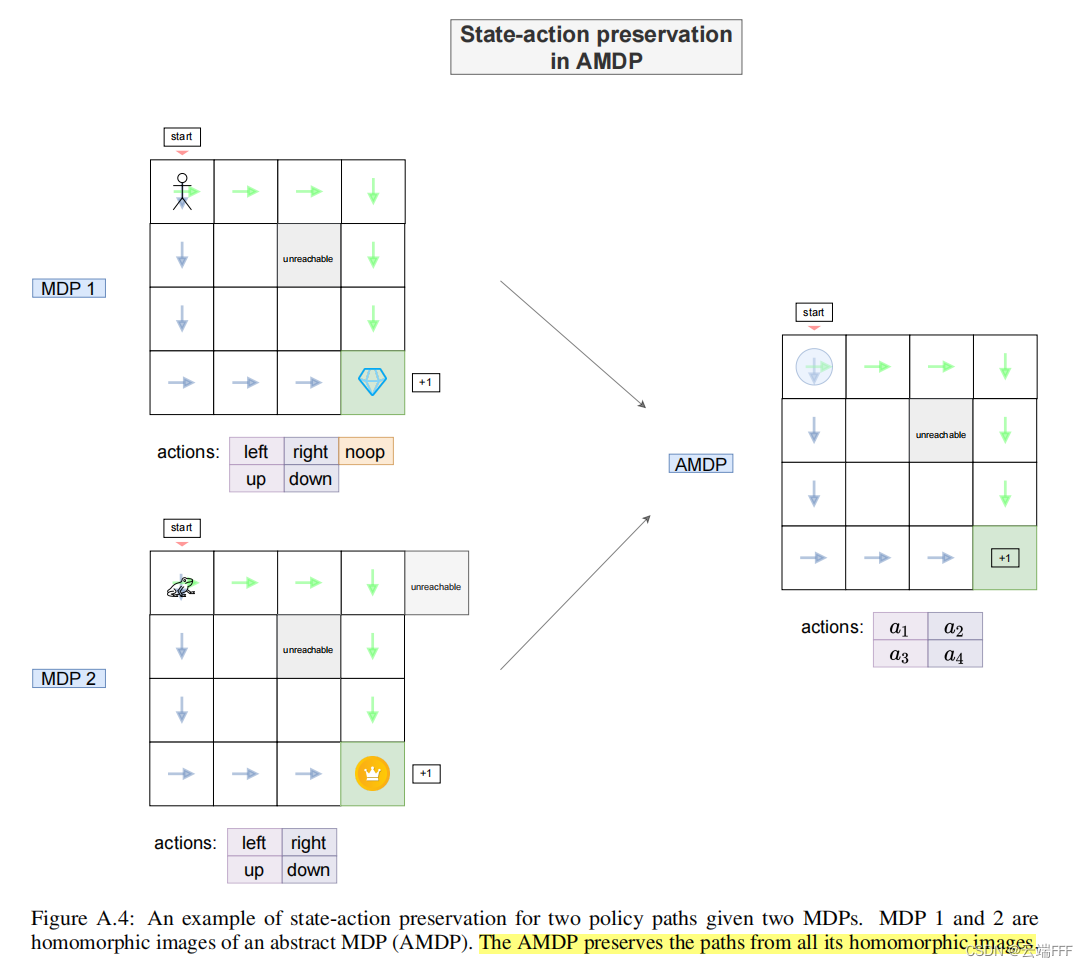
- 借助 AMDP,可以屏蔽状态、动作空间表示的差异,只去关注转移矩阵差异导致的 distribution shift
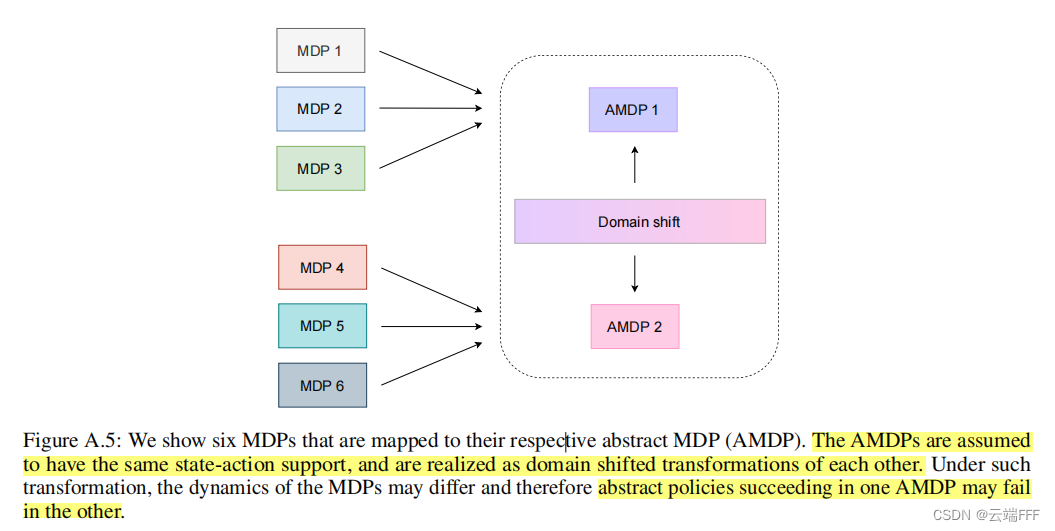
- 利用 AMDP,可以发现具体 MDP 间的 distribution shift 不是必然导致可行轨迹(策略)不同,有时会有时不会
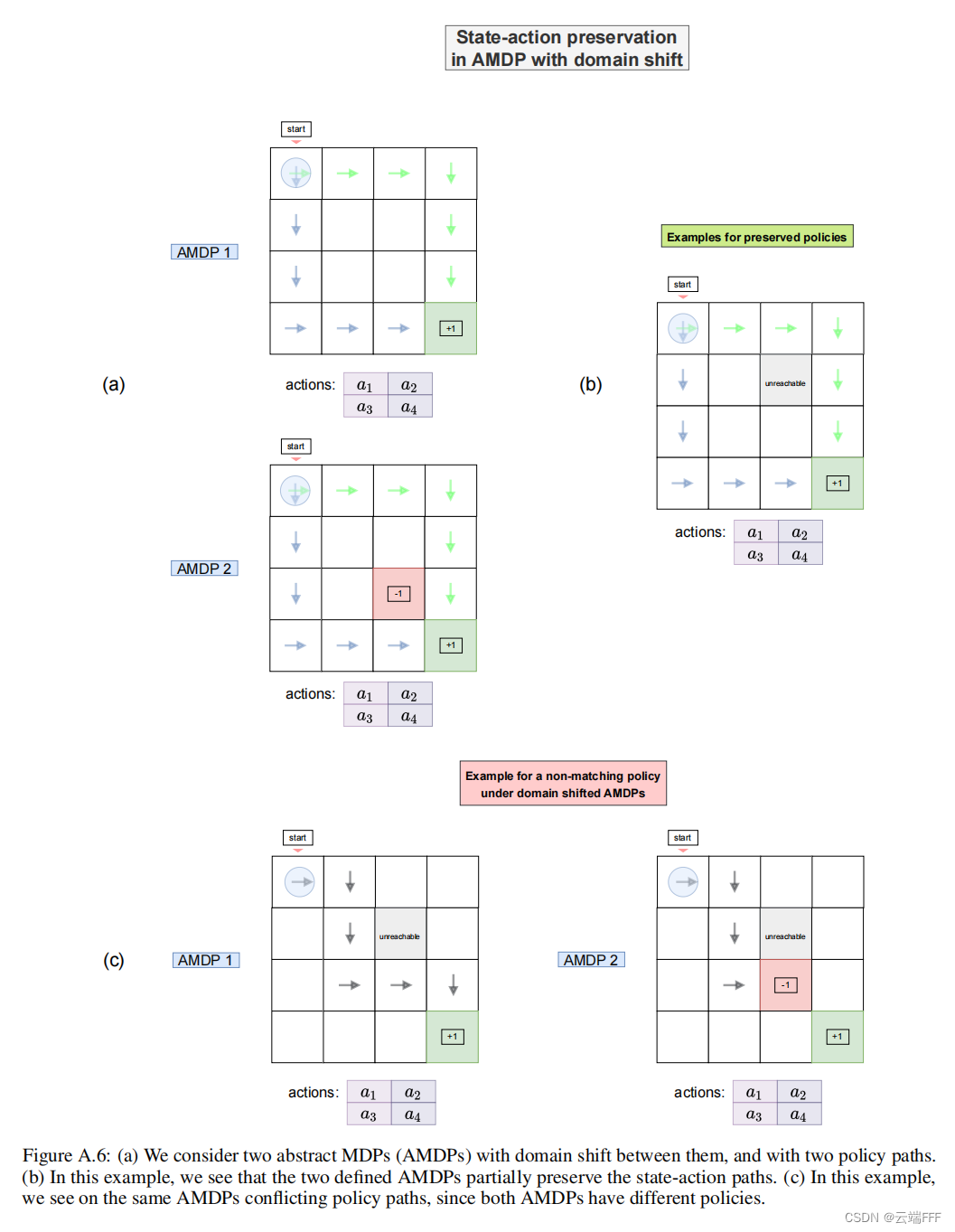
- 利用 AMDP 屏蔽表示形式的差异
-
注意,AMDP 只是对具体 MDP 状态空间和动作空间的抽象,并没有对转移矩阵做出要求(也就是说抽象前后的转移矩阵可以不同)。作者把多个具体 MDP 抽象为同一个 AMDP,本质上是想刻画具体 MDP 的微小变化,具体而言
- 认为 “动作空间的差异” 和 “状态空间的差异” 很小可以屏蔽掉,这步屏蔽就通过 AMDP 来实现
- 接下来可以只去关注 “转移矩阵的差异”,而 “转移矩阵的差异” 会体现在离线数据集中 transition 的分布上 ,下面只去考虑这个即可
2.2.2 利用 AMDP 说明两个指标的稳定性
- 如果多个具体 MDP 可以抽象为同一个 AMDP ,我们称这些 MDP 为这个 AMDP 的
同态图homomorphic images。可以证明:给定 AMDP M ^ \hat{M} M^ 和它的两个同态图 M , M ~ M,\tilde{M} M,M~(两个具体MDP),设三者的 transition 分布分别为 p ( s , a , r , s ′ ) , p ~ ( s ~ , a ~ , r , s ′ ~ ) , p ^ ( s ^ , a ^ , r , s ′ ^ ) p(s,a,r,s'),\space \tilde{p}(\tilde{s},\tilde{a},r,\tilde{s'}),\space \hat{p}(\hat{s},\hat{a},r,\hat{s'}) p(s,a,r,s′), p~(s~,a~,r,s′~), p^(s^,a^,r,s′^) ,transition熵差异的上界为
∣ H ( p ) − H ( p ~ ) ∣ ⩽ max [ H ( p ) , H ( p ~ ) ] − H ( p ^ ) (5) |H(p)-H(\tilde{p})| \leqslant \max [H(p), H(\tilde{p})]-H(\hat{p}) \tag{5} ∣H(p)−H(p~)∣⩽max[H(p),H(p~)]−H(p^)(5) 证明请参考原文。这样一来,我们用 AMDP 抽象过程考虑了状态动作空间的扰动,在上述定理中考虑了转移矩阵的扰动,等式(5)说明 MDP 发生微小扰动时transition熵指标的变化是稳定的 - 再考虑第二个指标,即离线数据集的期望轨迹return。因为转移矩阵可能变化,为了保持 behavior policy 尽量不变,作者这里认为 AMDP 的两个同态图(两个具体MDP)上的策略会映射到 AMDP 上相同的抽象策略,显然这时 AMDP 会保持公共的即时 reward
r
r
r,这种情况下,MDP 发生微小扰动
期望轨迹return指标不变
2.3 指标实用化
-
先小节一下之前的内容,作者提出了两个离线数据集特征指标,并证明了他们关于 MDP 扰动是稳定的
- 探索性指标 “transition熵”,确定性MDP中简化为 “占用度量熵”: H ( ρ π ( s , a ) ) : = − ∑ s , a ρ π ( s , a ) > 0 ρ π ( s , a ) log ( ρ π ( s , a ) ) H\left(\rho_{\pi}(s, a)\right):=-\sum_{\substack{s, a \\ \rho_{\pi}(s, a)>0}} \rho_{\pi}(s, a) \log \left(\rho_{\pi}(s, a)\right) H(ρπ(s,a)):=−s,aρπ(s,a)>0∑ρπ(s,a)log(ρπ(s,a))
- 利用性指标 “期望轨迹return”: g T : = E τ ∼ T [ ∑ t = 0 ∞ γ t r t ∣ r t ∈ τ ] g_\mathcal{T} := \mathbb{E}_{\tau\sim\mathcal{T}}\left[\sum_{t=0}^\infin\gamma^tr_t|r_t\in\tau\right] gT:=Eτ∼T[t=0∑∞γtrt∣rt∈τ]
这些指标难以直接计算,且无法跨 MDP 进行比较,下面进行简化和归一化处理,将他们改进为实用的度量标准
2.3.1 探索性指标:SACo
- 设我们用一个估计器去估计数据集
D
\mathcal{D}
D 的占用度量熵,得到的结果表示为
H
^
(
D
)
\hat{H}(\mathcal{D})
H^(D),再设数据集中含有不同
(
s
,
a
)
(s,a)
(s,a) pair 的数量为
u
s
,
a
(
D
)
u_{s,a}(\mathcal{D})
us,a(D)。我们知道没有任何限制时均匀分布的熵最大,因此有
H ^ ( D ) ≤ log ( u s , a ( D ) ) \hat{H}(\mathcal{D}) \leq \log(u_{s,a}(\mathcal{D})) H^(D)≤log(us,a(D)) 这时 log ( u s , a ( D ) ) \log(u_{s,a}(\mathcal{D})) log(us,a(D)) 可以看作确定性 MDP 的 Offline Dataset 探索性的上限。两边分别取 e 的指数,得到
e H ^ ( D ) ≤ u s , a ( D ) e^{\hat{H}(\mathcal{D})} \leq u_{s,a}(\mathcal{D}) eH^(D)≤us,a(D) 因为 x x x 和 e x e^x ex 是正相关的,所以某种程度上也可以直接把 u s , a ( D ) u_{s,a}(\mathcal{D}) us,a(D) 看作数据集探索性的指标Note:如果深究的话,形如 e H ^ ( D ) e^{\hat{H}(\mathcal{D})} eH^(D) 这种对熵取指数的操作,其实是 NLP 领域常用的一个指标,称为
困惑度perplexity。注意到熵可以看作 E X [ log 1 p ( x ) ] \mathbb{E}_X\left[\log\frac{1}{p(x)}\right] EX[logp(x)1],困惑度对它取指数就相当于 E X [ 1 p ( x ) ] \mathbb{E}_X\left[\frac{1}{p(x)}\right] EX[p(x)1]。NLP 里用测试集 X X X 评估模型 p p p 的好坏时会用到该指标,这时 p ( x ) p(x) p(x) 代表模型认为测试集中句子 x x x 出现的概率,测试集中的句子都是正常的句子,那么好的模型就是在测试集上的概率越高越好,句子越好,预测概率 p ( x ) p(x) p(x) 应该越大,困惑度 1 p ( x ) \frac{1}{p(x)} p(x)1 应该越小(也就是模型对句子越不困惑),所以困惑度越小 NLP 模型就可以认为越好 - 注意到数据集大小会影响到
u
s
,
a
(
D
)
u_{s,a}(\mathcal{D})
us,a(D) 取值,所以还需要用同 MDP 同尺寸的参考数据集
D
ref
\mathcal{D}_{\text{ref}}
Dref 进行规范化。实验中作者使用整个训练 online agent 进行数据收集过程中的 replay buffer 作为
D
ref
\mathcal{D}_{\text{ref}}
Dref,这样最后得到的实用度量 SACo 定义为
S A C o ( D ) = u s , a ( D ) u s , a ( D ref ) SACo(\mathcal{D}) = \frac{u_{s,a}(\mathcal{D})}{u_{s,a}(\mathcal{D_{\text{ref}}})} SACo(D)=us,a(Dref)us,a(D) 具体实践中,当数据集尺寸特别大时,对不同 ( s , a ) (s,a) (s,a) 进行计数是困难的,因此作者使用了 HyperLogLog 这个基于概率的计数方法,具体说明可以参考 HyperLogLog 算法详解
2.3.2 利用性指标:TQ
- 设离线数据集
D
\mathcal{D}
D 中含有
B
B
B 条轨迹,可以用经验平均代替数学期望,这个数据集的 “期望轨迹return” 可以估计为
g ˉ ( D ) = 1 B ∑ b = 0 B g τ b = 1 B ∑ b = 0 B ∑ t = 0 T b γ t r b , t \bar{g}(\mathcal{D}) = \frac{1}{B}\sum_{b=0}^B g_{\tau_b} = \frac{1}{B}\sum_{b=0}^B \sum_{t=0}^{T_b}\gamma^t r_{b,t} gˉ(D)=B1b=0∑Bgτb=B1b=0∑Bt=0∑Tbγtrb,t 再对它进行对应 MDP 上的 max-min 归一化,这样可以消除 reward 的取值范围的影响,实现跨 MDP 比较,这样最后得到的实用度量 TQ 定义为
T Q ( D ) : = g ˉ ( D ) − g ˉ ( D min ) g ˉ ( D expert ) − g ˉ ( D min ) T Q(\mathcal{D}):=\frac{\bar{g}(\mathcal{D})-\bar{g}\left(\mathcal{D}_{\min }\right)}{\bar{g}\left(\mathcal{D}_{\text {expert }}\right)-\bar{g}\left(\mathcal{D}_{\min }\right)} TQ(D):=gˉ(Dexpert )−gˉ(Dmin)gˉ(D)−gˉ(Dmin) 其中 D min \mathcal{D}_{\min } Dmin 和 D expert \mathcal{D}_{\text{expert} } Dexpert 分别是在该 MDP 上使用最差和最好策略收集轨迹数据构成的数据集。在实验中作者使用 online policy 训练中发现的最好策略作为 π expert \pi_{\text{expert}} πexpert,使用随机策略作为 π min \pi_{\min} πmin 来生成这两个数据集
3. 实验
3.1 生成数据集的方法
- 作者设计了五种生成数据集的方法,以系统地涵盖过去对 Offline RL 的研究。这里作者训练了一个 Online DQN Agent,用它和环境交互到收敛所使用的样本数作为 Offline 数据集大小,并且用它作为专家策略(如果需要专家的话)

- 注意到从同一个 MDP 中用不同方法生成不同数据集,可以解释成策略诱导的 transition 分布之间的 domain shift,作者进一步分析了生成 RL 数据集时可能发生的 domain shift。形式化地讲,这里 domain shift 可以定义成分布
p
(
s
,
a
,
r
,
s
′
)
p(s,a,r,s')
p(s,a,r,s′) 到
p
˘
(
s
,
a
,
r
,
s
′
)
\breve{p}(s,a,r,s')
p˘(s,a,r,s′) 之间的变化,注意到 transition 概率可以如下展开
p π ( s , a , r , s ) = p ( r ∣ s , a , s ′ ) p ( s ′ ∣ s , a ) p π ( a ∣ s ) ρ π ( s ) p_{\pi}(s, a, r, s)=p\left(r \mid s, a, s^{\prime}\right) p\left(s^{\prime} \mid s, a\right) p_{\pi}(a \mid s) \rho_{\pi}(s) pπ(s,a,r,s)=p(r∣s,a,s′)p(s′∣s,a)pπ(a∣s)ρπ(s) 其中三个条件概率分布的漂移对应三种可能的 domain shift

另外注意 ρ π ( s ) \rho_\pi(s) ρπ(s) 可以递归定义为 p π ( s ′ ) = ∑ s p π ( s ) ∑ a p π ( a ∣ s ) p ( s ′ ∣ s , a ) p_\pi(s')=\sum_sp_\pi(s)\sum_ap_\pi(a|s)p(s'|s,a) pπ(s′)=∑spπ(s)∑apπ(a∣s)p(s′∣s,a),所以状态的初始分布、策略分布以及状态动态分布的漂移都会导致 ρ π ( s ) \rho_\pi(s) ρπ(s) 的 domain shift,上述几种 domain shift 也可能以各种组合形式同时发生。总之,作者的结论就是对同一个 MDP 用不同 behavior policy 生成 Offline Dataset 会导致数据集中 transition 分布发生 domain shift,这个其实很直观了,从 1.2 节的可视化图上也能看出来
3.2 实验结果
3.2.1 数据集特征对比
- 作者对比了几种不同方式生成的 Offline Dataset 的 TQ 和 SACo,如下
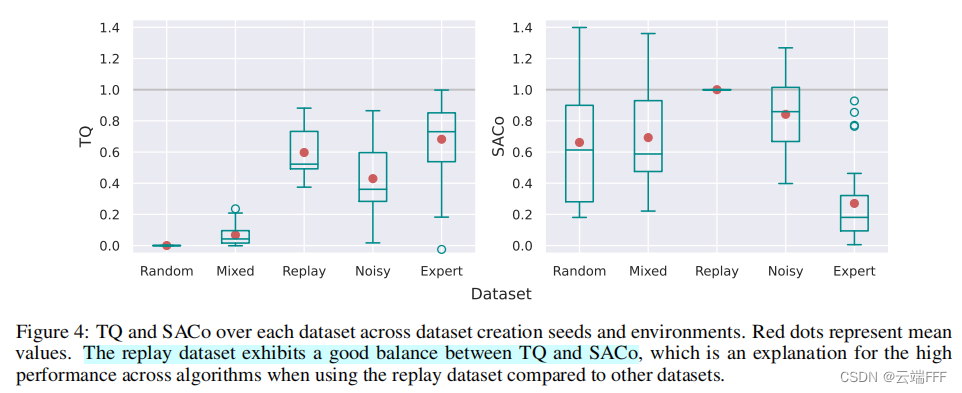
可见专家数据集期望return较高,transition熵较小;随机数据集与之正好相反;replay buffer 数据集在两者间取得平衡。这是符合预期的
3.2.2 数据集特征对 Offline RL 算法的影响
- 作者使用上述 5 种方法,对来自 gym、MiniGrid 和 MinAtar 的 6 个确定性环境生成了 150 个离线数据集,并在不同离线数据集上运行了 9 种 Offline RL 算法,结果如下
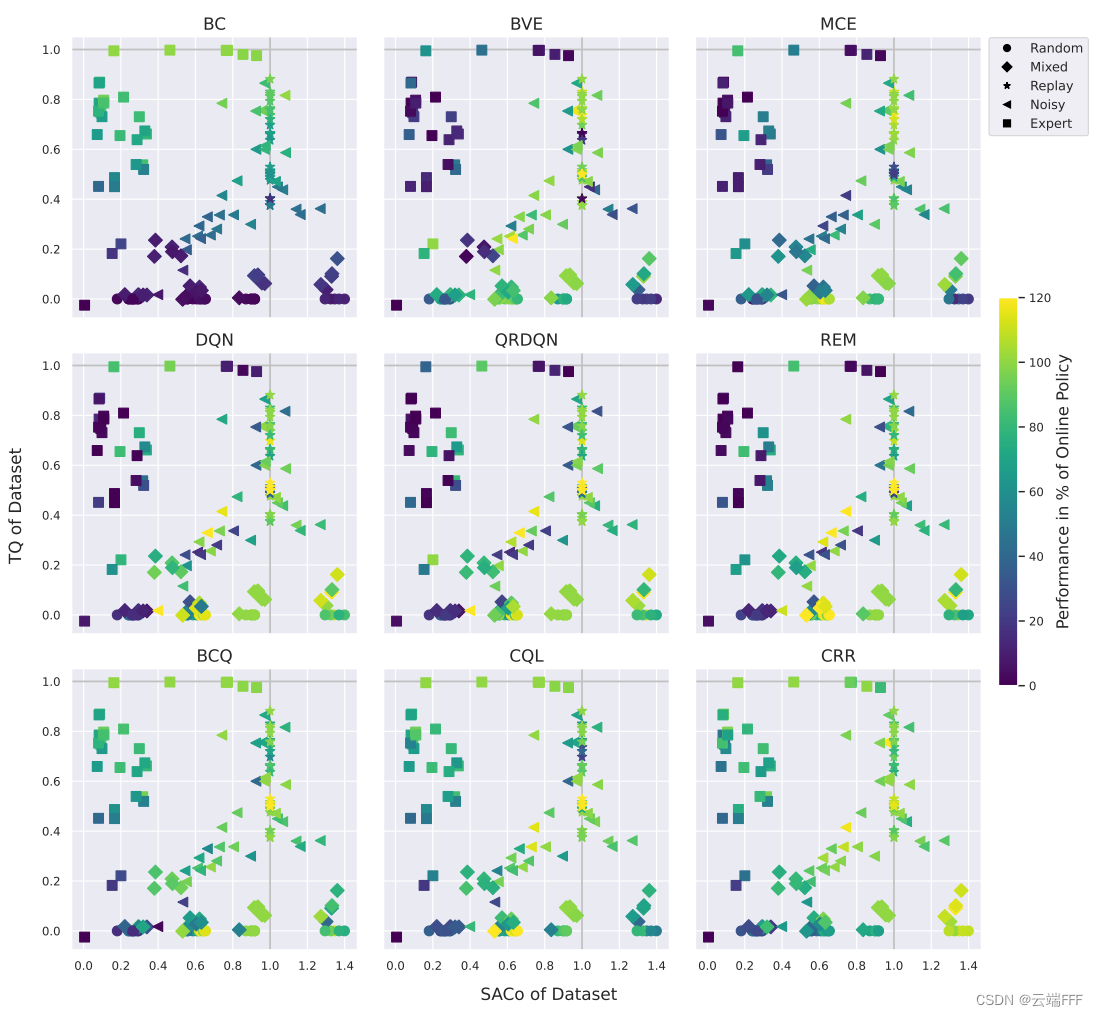
这里每个子图代表一个算法,每个点代表一个 Offline Dataset(因此在所有子图中位置相同),点的颜色代表 Offline RL 算法取得的最佳性能占 Online DQN Baseline 方法性能的比例。其中 Offline RL 算法性能如下计算
ω ( D offline ) = g ˉ ( D offline ) − g ˉ ( D min ) g ˉ ( D expert ) − g ˉ ( D min ) \omega\left(\mathcal{D}_{\text {offline }}\right)=\frac{\bar{g}\left(\mathcal{D}_{\text {offline }}\right)-\bar{g}\left(\mathcal{D}_{\text {min }}\right)}{\bar{g}\left(\mathcal{D}_{\text {expert }}\right)-\bar{g}\left(\mathcal{D}_{\min }\right)} ω(Doffline )=gˉ(Dexpert )−gˉ(Dmin)gˉ(Doffline )−gˉ(Dmin ) 观察到- 离线数据集特征和 3.2.1 节分析一致
- DQN 类方法 (DQN, QRDQN, REM) 需要高 SACo 的离线数据集,才能得到好的性能
- 只有离线数据集具有高 TQ 时,BC 方法才能 work
- BVE 和 MCE 对特定的环境和数据集设置非常敏感,总体上看更偏好 SACo 值较高的数据集
- BCQ, CQL 和 CRR 等策略约束方法要求最终策略贴近 behavior policy,因此在低 SACo 高 TQ 的环境中比 DQN 类方法更好,另外它们在 “高SACo高TQ” 和 “中SACo中TQ” 的环境表现也不错
4. 总结
- 本文作者提出了两个离线数据集特征指标:“transition熵” 和 “期望轨迹return”,证明了他们关于 MDP 扰动是稳定的,然后给出对应的两个实用度量 SACo 和 TQ。利用这两个指标,作者发现 Offline RL 中的流行算法会受到数据集特征的强烈影响,不同数据集之间的平均性能可能不足以进行公平的比较
- 本文的几个问题在于
- 只考虑的确定性 MDP
- 只对比分析了 Model-free 的 Offline RL 算法
- 只用 DQN 作为 Online Baseline
- 熵指标简化为不同 ( s , a ) (s,a) (s,a) pair 计数,这个简化可能影响指标精度
- 对于数据集生成过程中的 domain shift 可以进一步研究,这个其实是影响 Offline RL 算法的关键
