0 写在前面

机器学习强基计划聚焦深度和广度，加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理；“广”在分析多个机器学习模型：决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。强基计划实现从理论到实践的全面覆盖，由本人亲自从底层编写、测试与文章配套的各个经典算法，不依赖于现有库，可以大大加深对算法的理解。

🚀详情：机器学习强基计划(附几十种经典模型源码)

1 高斯概率密度

高斯分布又叫正态分布，是一个在理科、工科、文科等多个领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力，具有：

• 集中性：正态曲线的高峰位于正中央
• 对称性：正态曲线以均值为中心，左右对称
• 均匀性：正态曲线从均值处开始，分别向左右两侧逐渐均匀下降

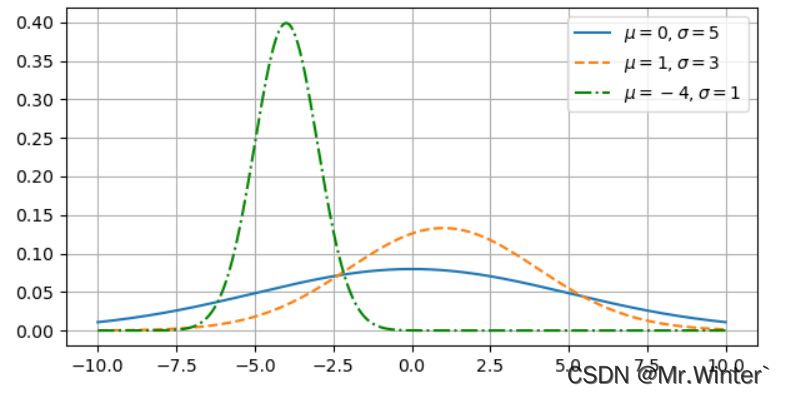
高斯分布的表达式是

$$f\left(x\right)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}\right)$$

其中$\mu$是均值，$\sigma$是标准差

2 混合高斯分布

混合高斯模型(Gaussian Mixture Model)是通过一定的权重将多个单高斯分布加权而成的混合概率模型，使模型容量更大，产生更复杂的采样或拟合更复杂的分布。

混合高斯分布的表达式很容易理解：

$$p_{\mathcal{M}}\left(\mathbf{x}\right)=\sum _{j=1}^k{\pi }_{j}P\left(\mathbf{x}|{\mathbf{\mu }}_j,{\Sigma }_j\right)$$

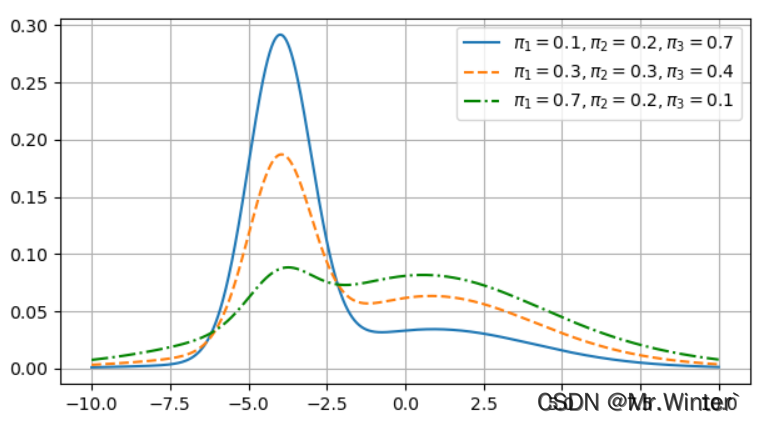
其中${\sum }_{j=1}^k{\pi }_j=1$，将第一节的三个高斯分布以一定权重加权得到下图所示的混合高斯分布

3 GMM算法

3.1 定义

高斯混合聚类基于极大似然法，采用一组原型分布来刻画数据聚合结构。在基于原型向量的原型聚类中，与原型向量最接近的样本被划分为簇；在GMM中，则将最有可能由原型分布产生的样本划分为簇

样本$\mathbf{x}$符合上述的混合高斯分布

$$p_{\mathcal{M}}\left(\mathbf{x}\right)=\sum _{j=1}^{k}P\left(\mathbf{x},z|{\mathbf{\mu }}_j,{\Sigma }_j\right)=\sum _{j=1}^{k}P\left(z|{\mathbf{\mu }}_j,{\Sigma }_j\right)P\left(\mathbf{x}|{\mathbf{\mu }}_j,{\Sigma }_j\right)$$

其中$P\left(\mathbf{x}|{\mathbf{\mu }}_j,{\Sigma }_j\right)$为高斯分布

$$P\left(\mathbf{x}|{\mathbf{\mu }}_j,{\Sigma }_j\right)=\frac{1}{{\left(2\pi \right)}^{d/2}{\left|{\Sigma }_j\right|}^{1/2}}\exp \left(-\frac{1}{2}{\left(\mathbf{x}-{\mathbf{\mu }}_j\right)}^T{\Sigma }_j^{-1}\left(\mathbf{x}-{\mathbf{\mu }}_j\right)\right)$$

隐变量$z_i$为样本$\mathbf{x}$所属的簇标记，也是我们要学习的参数。$P\left(\mathbf{x}|{\mathbf{\mu }}_j,{\Sigma }_j\right)$与$P\left(z|{\mathbf{\mu }}_j,{\Sigma }_j\right)$独立，因为隐式地为$\mathbf{x}$赋予标记不会影响$\mathbf{x}$由某个高斯分布分量$N_j\left({\mathbf{\mu }}_j,{\Sigma }_j\right)$产生的概率。进一步，定义由$N_j\left({\mathbf{\mu }}_j,{\Sigma }_j\right)$产生样本的簇标记就为$j$，即$P\left(z|{\mathbf{\mu }}_j,{\Sigma }_j\right)=P\left(z=j\right)$，记为$\alpha$。混合高斯分布简化为

$$p_{\mathcal{M}}\left(\mathbf{x}\right)=\sum _{j=1}^k{\alpha }_{j}P\left(\mathbf{x}|{\mathbf{\mu }}_j,{\Sigma }_j\right)$$

其中${\sum }_{j=1}^k{\alpha }_j=1$

3.2 参数估计

对于模型参数待估计且隐变量分布未知的情形，采用EM算法迭代求解。这部分的推导请看机器学习强基计划6-4：详细推导期望最大化EM算法及收敛性分析(附实例)，通过EM算法可以得到

$${\mathbf{\mu }}_j=\frac{{\sum }_{i=1}^m{\gamma }_{ij}{\mathbf{x}}_i}{{\sum }_{i=1}^m{\gamma }_{ij}}$$

$${\Sigma }_j=\frac{{\sum }_{i=1}^m\begin{array}{c}{\gamma }_{ij}\left({\mathbf{x}}_i-{\mathbf{\mu }}_j\right)\end{array}{\left({\mathbf{x}}_i-{\mathbf{\mu }}_j\right)}^T}{{\sum }_{i=1}^m\begin{array}{c}{\gamma }_{ij}\end{array}}$$

其中${\gamma }_{ij}\left(j=1,2,\cdots ,k\right)$是经过E步计算得到的$Q\left({\mathbf{z}}_i\right)$

对于$\alpha$，由于其需要在满足${\sum }_{j=1}^k{\alpha }_j=1$的前提下最大化似然，因此引入拉格朗日形式

$$LL\left(\mathbf{\theta },\lambda \right)=L\left(\mathbf{\theta }\right)+\lambda \left(\sum _{j=1}^k{\alpha }_j-1\right)$$

其中$\lambda$为拉格朗日算子。令$\partial LL\left(\mathbf{\theta },\lambda \right)/\partial {\alpha }_j=0$，则

$$\frac{\partial LL\left(\mathbf{\theta },\lambda \right)}{\partial {\alpha }_j}=\frac{\partial L\left(\mathbf{\theta }\right)}{\partial {\alpha }_j}+\lambda =\sum _{i=1}^m\frac{{\gamma }_{ij}}{{\alpha }_j}+\lambda =0$$

即得${\alpha }_j=-{\sum }_{i=1}^m{\gamma }_{ij}/\lambda$。注意到等式${\sum }_{i=1}^m{\gamma }_{ij}/{\alpha }_j+\lambda =0$两边对$k$个高斯分量求和可得

$$\sum _{j=1}^k\sum _{i=1}^m{\gamma }_{ij}+\lambda \sum _{j=1}^k{\alpha }_j=0\Rightarrow \sum _{i=1}^m\sum _{j=1}^k{\gamma }_{ij}+\lambda =0\Rightarrow \lambda =-m$$

所以

$${\alpha }_j=-\frac{1}{m}\sum _{i=1}^m{\gamma }_{ij}$$

4 Python实现

4.1 算法流程

4.2 E步

gamma = []  # 后验概率 i x j
for i in range(self.m):
    gammaSum = 0
    for j in range(self.k):
        gammaSum = gammaSum + self.alpha[j] * self.__gauss(self.dataSet[i], self.miu[j], self.sigma[j])
    for j in range(self.k):
        gamma.append(self.alpha[j] * self.__gauss(self.dataSet[i], self.miu[j], self.sigma[j]) / gammaSum)

4.3 M步

• 更新均值向量

  for j in range(self.k):
     miuTemp = np.zeros_like(self.miu[0])
     for i in range(self.m):
         miuTemp = miuTemp + gamma[i * self.k + j] * self.dataSet[i]
         gammaTemp = gammaTemp + gamma[i * self.k + j]
     gammaTempList.append(gammaTemp)
     self.miu[j] = miuTemp / gammaTemp
     gammaTemp = 0
  

• 更新协方差矩阵

  for j in range(self.k):
  sigmaTemp = np.zeros_like(self.sigma[0])
  for i in range(self.m):
      sigmaTemp = sigmaTemp + gamma[i * self.k + j] * np.array(self.dataSet[i] - self.miu[j]).reshape([self.dim, 1]) * \
                  np.array(self.dataSet[i] - self.miu[j]).reshape([1, self.dim]) 
  self.sigma[j] = sigmaTemp / gammaTempList[j]
  

• 更新混合系数

  for j in range(self.k):
      self.alpha[j] = gammaTempList[j] / self.m
  

和算法流程一一对应，可对照学习加深理解

4.4 可视化

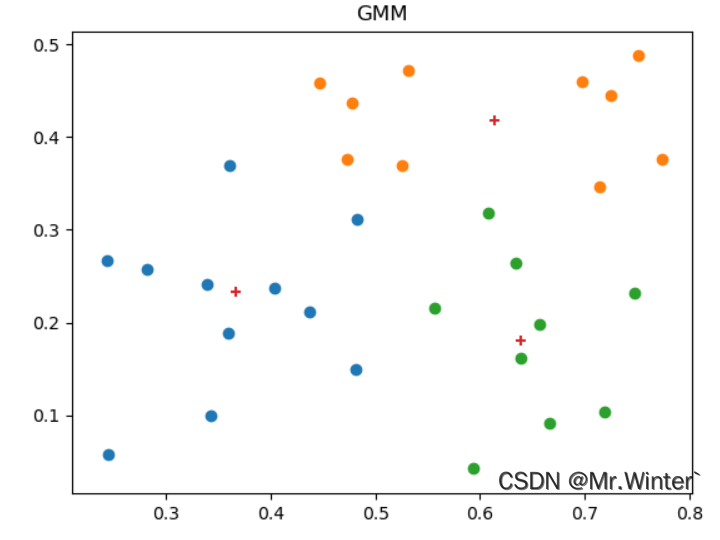
本文完整工程代码联系下方博主名片获取

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《机器人原理与技术》
• 《机器学习强基计划》
• 《计算机视觉教程》
• …