STL容器 —— map和set的模拟实现
文章目录
- 1. 红黑树的框架
- 2. 模板参数的一些细节
- 3. 红黑树支持迭代器
- 3.1 迭代器的实现
- 3.1.1 解引用
- 3.1.2 == 和 !=
- 3.1.3 ++ 和 - -
- 3.2 红黑树封装迭代器
- 3.2.1 修改一下insert
- 3.2.2 迭代器的 begin(),end()
- 3.2.3 修改一下find函数,返回迭代器
- 4. 红黑树继续完善
- 4.1 红黑树的拷贝构造和赋值重载
- 4.2 红黑树的析构函数
- 5. 封装红黑树的map和set
- 5.1 map的模拟实现
- 5.2 set的模拟实现
- 6. 总结
前言: map和set的底层是用红黑树实现的,红黑树的大框架,在我的上一篇博客: 红黑树的实现 中已经详细的讲解了,但是对于支持实现map和set还是欠缺的,比如 :迭代器,模板参数等,还需要再继续完善。这样才能够 模拟实现 map和set。
1. 红黑树的框架
#include<iostream>
#include<assert.h>
namespace RB_tree
{
enum Color
{
Red,
Black
};
template<class K, class V>
struct RBtree_node
{
RBtree_node<K, V>* left_;
RBtree_node<K, V>* right_;
RBtree_node<K, V>* parents_;
std::pair<K, V> kv_;
Color col_;
RBtree_node(const std::pair<K, V>& kv)
:left_(nullptr),
right_(nullptr),
parents_(nullptr),
kv_(kv),
col_(Red)
{}
};
template<class K, class V>
class RBtree
{
typedef RBtree_node<K, V> Node;
private:
Node* _root;
public:
RBtree()
:_root(nullptr)
{}
public:
bool insert(const std::pair<K, V>& node)
{
if (_root == nullptr)
{
_root = new Node(node);
_root->col_ = Black;
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (node.first > cur->kv_.first)
{
parent = cur;
cur = cur->right_;
}
else if (node.first < cur->kv_.first)
{
parent = cur;
cur = cur->left_;
}
else
{
assert(false);
}
}
cur = new Node(node);
cur->col_ = Red;
if (parent->kv_.first > cur->kv_.first)
{
parent->left_ = cur;
cur->parents_ = parent;
}
else
{
parent->right_ = cur;
cur->parents_ = parent;
}
while (parent && parent->col_ == Red)
{
Node* grand = parent->parents_;
/// 插入到左树
if (parent == grand->left_)
{
Node* uncle = grand->right_;
/// 情况一
if (uncle && uncle->col_ == Red)
{
parent->col_ = Black;
uncle->col_ = Black;
grand->col_ = Red;
/// 往上更新
cur = grand;
parent = cur->parents_;
}
/// 情况二 或情况三
else
{
右单旋
if (cur == parent->left_)
{
revolov_R(grand);
parent->col_ = Black;
grand->col_ = Red;
}
else
{
revolov_L(parent);
revolov_R(grand);
cur->col_ = Black;
grand->col_ = Red;
}
break;
}
}
/// 插入到右树
else
{
Node* uncle = grand->left_;
/// 情况一
if (uncle && uncle->col_ == Red)
{
parent->col_ = Black;
uncle->col_ = Black;
grand->col_ = Red;
/// 往上更新
cur = grand;
parent = cur->parents_;
}
else
{
左单旋
if (cur == parent->right_)
{
revolov_L(grand);
parent->col_ = Black;
grand->col_ = Red;
}
else
{
revolov_R(parent);
revolov_L(grand);
cur->col_ = Black;
grand->col_ = Red;
}
break;
}
}
}
_root->col_ = Black;
return true;
}
private:
void revolov_R(Node* issue_node)
{
Node* issue_Lnode = issue_node->left_;
Node* issue_Lnode_R = issue_Lnode->right_;
Node* issue_node_parent = issue_node->parents_;
issue_node->left_ = issue_Lnode_R;
if (issue_Lnode_R)
{
issue_Lnode_R->parents_ = issue_node;
}
issue_Lnode->right_ = issue_node;
issue_node->parents_ = issue_Lnode;
if (issue_node_parent == nullptr)
{
_root = issue_Lnode;
issue_Lnode->parents_ = nullptr;
}
else
{
if (issue_node_parent->left_ == issue_node)
issue_node_parent->left_ = issue_Lnode;
else
issue_node_parent->right_ = issue_Lnode;
issue_Lnode->parents_ = issue_node_parent;
}
}
void revolov_L(Node* issue_node)
{
Node* issue_Rnode = issue_node->right_;
Node* issue_Rnode_L = issue_Rnode->left_;
Node* issue_node_parent = issue_node->parents_;
issue_node->right_ = issue_Rnode_L;
if (issue_Rnode_L)
{
issue_Rnode_L->parents_ = issue_node;
}
issue_Rnode->left_ = issue_node;
issue_node->parents_ = issue_Rnode;
if (issue_node_parent == nullptr)
{
_root = issue_Rnode;
issue_Rnode->parents_ = nullptr;
}
else
{
if (issue_node_parent->left_ == issue_node)
issue_node_parent->left_ = issue_Rnode;
else
issue_node_parent->right_ = issue_Rnode;
issue_Rnode->parents_ = issue_node_parent;
}
}
public:
void InOrder()
{
_InOrder(_root);
}
private:
void _InOrder(Node* root)
{
if (root == NULL)
return;
_InOrder(root->left_);
std::cout << root->kv_.first << ":" << root->kv_.second << std::endl;
_InOrder(root->right_);
}
};
}
2. 模板参数的一些细节
底层 set中红黑树的节点 不是键值对,单一的一个类型;map中红黑树的节点 是一个键值对。所以需要创建两个版本的红黑树吗?答案是不需要,可以利用模板来支持泛型的。
我们需要对 红黑树的节点的 模板参数 做一下修改:
这样 就能够通过模板参树 来控制 节点的类型
template<class T>
struct RBtree_node
{
RBtree_node<T>* left_;
RBtree_node<T>* right_;
RBtree_node<T>* parents_;
T kv_;
Color col_;
RBtree_node(const T & kv)
:left_(nullptr),
right_(nullptr),
parents_(nullptr),
kv_(kv),
col_(Red)
{}
};
- set的基本框架
template<class K>
class set
{
private:
RBtree<K,K,setketofT> t_;
public:
struct setketofT
{
const K& operator()(const K& k)
{
return k;
}
};
};
- map的基本框架
template<class K,class V>
class map
{
private:
RBtree<K, std::pair<K, V>,mapkofT> t_;
public:
struct mapkofT
{
const K& operator()(const std::pair<K,V>& t)
{
return t.first;
}
};
};
可以看到在基本框架里面:给红黑树多传了一个模板参数 分别是setketofT,mapkofT。它们是仿函数,目的是 让红黑树顺利的取出,节点的类型,然后可以进行插入等操作。map传的是 pair的first;set传的是 k。这个有点难理解,下面还会讲到的。
- set的底层:RBtree<K,K,setketofT> t_;
- map的底层:RBtree<K, std::pair<K, V>,mapkofT> t_;
红黑树的模板参数 也需要变动:
// 第三个模板参数用于接收 仿函数
template<class K, class T,class keyofT>
class RBtree
{
typedef RBtree_node<T> Node;
}
keyofT就是用来接收 仿函数的,它的作用就是 拿出 构建红黑树 需要比较的那个值,比如 set就是 拿的 k 做比较,map拿的是 pair<>的first进行比较。
3. 红黑树支持迭代器
首先一般情况下迭代器是个指针,比如 vector,string的迭代器,但是对于某些容器,需要对迭代器进行封装,从而使得此迭代器达到类似指针的功能,比如list,链表 对它指针 执行 ++ 操作,它是不能够 指向 下一个节点的,所以 它的迭代器就不能是一个单纯的指针,需要封装出一个类(迭代器),来实现 指针的操作,比如 ++ 迭代器 ,它就能指向list中下一个节点位置。
红黑树也是如此,我们也需要封装一个迭代器,实现 ++ ,- -,*,-> 的操作。红黑树迭代器走的是一个中序,这很关键,有了这个概念,我们才能开始 实现 迭代器的基本框架。
3.1 迭代器的实现
template<class T,class Ref,class Ptr>
struct RBtree_Iterator
{
typedef RBtree_node<T> Node;
typedef RBtree_Iterator<T, Ref, Ptr> self;
Node* node_;
RBtree_Iterator(Node* node)
:node_(node)
{}
self& operator++()
{
/// 如果右树不为空,那么下一个位置就是右树的最左节点
if (node_->right_ != nullptr)
{
Node* min = node_->right_;
while (min->left_)
{
min = min->left_;
}
node_ = min;
}
// 如果右树为空,那么有两种情况
else
{
Node* cur = node_;
Node* parent = cur->parents_;
while (parent && cur == parent->right_)
{
cur = parent;
parent = cur->parents_;
}
node_ = parent;
}
return *this;
}
self& operator--()
{
/// 如果左树不为空,那么下一个位置就是左树的最右节点
if (node_->left_ != nullptr)
{
Node* max = node_->left_;
while (max->right_)
{
max=max->right_;
}
node_ = max;
}
// 如果左树为空,那么有两种情况
else
{
Node* cur = node_;
Node* parent = cur->parents_;
while (parent && cur == parent->left_)
{
cur = parent;
parent = cur->parents_;
}
node_ = parent;
}
return *this;
}
Ref operator*()
{
return node_->kv_;
}
Ptr operator->()
{
return &node_->kv_;
}
bool operator ==(const self& n) const
{
return n.node_ == node_;
}
bool operator !=(const self& n) const
{
return n.node_ != node_;
}
};
上面就是迭代器的实现,它的底层就是 个节点指针:
然后 实现具体的功能:
3.1.1 解引用
Ref operator*()
{
return node_->kv_;
}
Ptr operator->()
{
return &node_->kv_;
}
大家可能对 这个返回值 Ref 和 Ptr 有疑问,我们先来看个这个迭代器类的模板参数:
template<class T,class Ref,class Ptr>
第一个 模板参数T 是用来 定义迭代器中 底层指针 的类型的。
第二个模板参数Ref,以及第三个模板参数 Ptr是为了支持 const版本的迭代器所使用的。
如果 不需要支持 const版本,那么 就可以这样写:
T& operator*()
{
return node_->kv_;
}
T* operator->()
{
return &node_->kv_;
}
但是要求支持const迭代器,怎么办?有两种方式,可以在写个const版本的迭代器,但是代码冗余;或者通过模板参数传参,来控制这块的返回值。
于是红黑树中,定义迭代器可以这样:
typedef RBtree_Iterator<T, T&, T*> iterator;
typedef RBtree_Iterator<T, const T&, const T*> const_iterator;
3.1.2 == 和 !=
bool operator ==(const self& n) const
{
return n.node_ == node_;
}
bool operator !=(const self& n) const
{
return n.node_ != node_;
}
这个比较简单,唯一有点需要理解的就是 self:
typedef RBtree_Iterator<T, Ref, Ptr> self;
这就是 迭代器 本身,所以 == ,!= 比较的是 两迭代器是否相等。
3.1.3 ++ 和 - -
self& operator++()
{
/// 如果右树不为空,那么下一个位置就是右树的最左节点
if (node_->right_ != nullptr)
{
Node* min = node_->right_;
while (min->left_)
{
min = min->left_;
}
node_ = min;
}
// 如果右树为空,那么有两种情况
else
{
Node* cur = node_;
Node* parent = cur->parents_;
while (parent && cur == parent->right_)
{
cur = parent;
parent = cur->parents_;
}
node_ = parent;
}
return *this;
}
self& operator--()
{
/// 如果左树不为空,那么下一个位置就是左树的最右节点
if (node_->left_ != nullptr)
{
Node* max = node_->left_;
while (max->right_)
{
max=max->right_;
}
node_ = max;
}
// 如果左树为空,那么有两种情况
else
{
Node* cur = node_;
Node* parent = cur->parents_;
while (parent && cur == parent->left_)
{
cur = parent;
parent = cur->parents_;
}
node_ = parent;
}
return *this;
}
这是实现这个迭代器比较难的部分,当然应该都知道,map和set迭代器走的是中序,所以这里也得按照中序的规则,来进行迭代器的++ 、- -。
中序就是 左子树 根 右子树.
我们通过画图,来理解 :
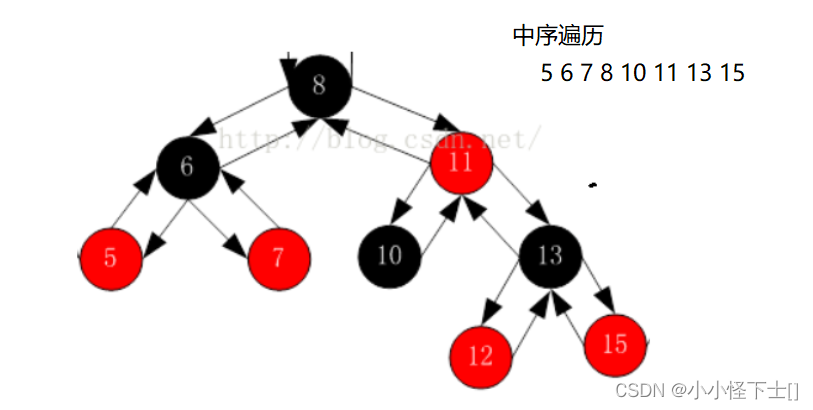
先是 ++ :
(1) 如果当下节点的右树存在,那么 此节点的下一个节点就是 其右树的最左节点:
比如当下节点 是 6节点,那么它的右子树还存在,但是右子树的左子树 不存在,所以右子树就是它的下一个节点。
比如当下节点是 8节点,那么它的右子树还存在,右子树的最左节点是10节点,所以它的下一个节点是10节点。
(2) 如果当下节点的右树不存在,那么 此节点的下一个节点就是 孩子在父亲的左边的 第一个祖先
这句话有点绕口,不过 看例子也能明白:
比如 5节点 它的右树为空 ,它下一个节点 就是它的父亲,因为它在 父亲的左。
比如 7节点 它的右树为空,它的下一个节点是谁?是它的父亲吗?
7节点的下一个节点是 8节点,8节点是它的祖先,并且7节点在它的左。代码实现的话,靠的是更新 当下节点,一直等到 祖先为空,或者第一次出现 当下节点在父亲节点的左。
self& operator++()
{
/// 如果右树不为空,那么下一个位置就是右树的最左节点
if (node_->right_ != nullptr)
{
Node* min = node_->right_;
while (min->left_)
{
min = min->left_;
}
node_ = min;
}
// 如果右树为空,那么有两种情况
else
{
Node* cur = node_;
Node* parent = cur->parents_;
while (parent && cur == parent->right_)
{
// 往上更新
cur = parent;
parent = cur->parents_;
}
node_ = parent;
}
return *this;
}
然后看 - -:
其实它逻辑就是上面 ++ 反一下,它也分两种情况:
(1) 如果当下节点的左树存在,那么 此节点的 上一个节点就是 其左树的最右节点
(2) 如果当下节点的右树不存在,那么 此节点的上一个节点就是 孩子在父亲的右边的 第一个祖先
self& operator--()
{
/// 如果左树不为空,那么下一个位置就是左树的最右节点
if (node_->left_ != nullptr)
{
Node* max = node_->left_;
while (max->right_)
{
max=max->right_;
}
node_ = max;
}
// 如果左树为空,那么有两种情况
else
{
Node* cur = node_;
Node* parent = cur->parents_;
while (parent && cur == parent->left_)
{
cur = parent;
parent = cur->parents_;
}
node_ = parent;
}
return *this;
}
3.2 红黑树封装迭代器
红黑树对迭代器进行封装,也就是说 要利用上面实现的迭代器 搞点事情:
template<class K, class T,class keyofT>
struct RBtree
{
typedef RBtree_node<T> Node;
public:
typedef RBtree_Iterator<T, T&, T*> iterator;
typedef RBtree_Iterator<T, const T&, const T*> const_iterator;
private:
Node* _root;
public:
iterator begin()
{
Node* cur = _root;
while(cur && cur->left_)
{
cur = cur->left_;
}
return iterator(cur);
}
iterator end()
{
return iterator(nullptr);
}
public:
RBtree()
:_root(nullptr)
{}
~RBtree()
{
destroy(_root);
_root = nullptr;
}
RBtree(const RBtree<K,T,keyofT>& n)
{
_root = copy(n->_root);
}
RBtree<K,T,keyofT>& operator = (RBtree<K,T,keyofT> n)
{
std::swap(_root,n._root);
return *this;
}
public:
void destroy(Node* root)
{
if (root == nullptr)
{
return ;
}
destroy(root->left_);
destroy(root->right_);
delete root;
}
Node* copy(Node* root)
{
if (_root == nullptr)
{
return nullptr;
}
Node* newnode = new Node(root->kv_);
newnode->col_ = root->col_;
newnode->left_ = copy(root->left_);
newnode->right_ = copy(root->right_);
if (newnode->left_)
{
newnode->left_->parents_ = newnode;
}
if (newnode->right_)
{
newnode->right_->parents_ = newnode;
}
return newnode;
}
iterator find(const K& key)
{
Node* cur = _root;
keyofT kot;
while (cur)
{
if (key > kot(cur->kv_))
{
cur = cur->right_;
}
else if (key > kot(cur->kv_))
{
cur = cur->left_;
}
else
{
return iterator(cur);
}
}
return end();
}
std::pair<iterator,bool> insert(const T& node)
{
if (_root == nullptr)
{
_root = new Node(node);
_root->col_ = Black;
return std::make_pair(iterator(_root),true);
}
keyofT kot;
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (kot(node)> kot(cur->kv_))
{
parent = cur;
cur = cur->right_;
}
else if (kot(node) < kot(cur->kv_))
{
parent = cur;
cur = cur->left_;
}
else
{
return std::make_pair(iterator(cur), false);
}
}
cur = new Node(node);
Node* newnode = cur;
cur->col_ = Red;
if (kot(parent->kv_) > kot(cur->kv_))
{
parent->left_ = cur;
cur->parents_ = parent;
}
else
{
parent->right_ = cur;
cur->parents_ = parent;
}
while (parent && parent->col_ == Red)
{
Node* grand = parent->parents_;
/// 插入到左树
if (parent == grand->left_)
{
Node* uncle = grand->right_;
/// 情况一
if (uncle && uncle->col_ == Red)
{
parent->col_ = Black;
uncle->col_ = Black;
grand->col_ = Red;
/// 往上更新
cur = grand;
parent = cur->parents_;
}
/// 情况二 或情况三
else
{
右单旋
if (cur == parent->left_)
{
revolov_R(grand);
parent->col_ = Black;
grand->col_ = Red;
}
else
{
revolov_L(parent);
revolov_R(grand);
cur->col_ = Black;
grand->col_ = Red;
}
break;
}
}
/// 插入到右树
else
{
Node* uncle = grand->left_;
/// 情况一
if (uncle && uncle->col_ == Red)
{
parent->col_ = Black;
uncle->col_ = Black;
grand->col_ = Red;
/// 往上更新
cur = grand;
parent = cur->parents_;
}
else
{
左单旋
if (cur == parent->right_)
{
revolov_L(grand);
parent->col_ = Black;
grand->col_ = Red;
}
else
{
revolov_R(parent);
revolov_L(grand);
cur->col_ = Black;
grand->col_ = Red;
}
break;
}
}
}
_root->col_ = Black;
return std::make_pair(iterator(newnode),true);
}
};

这里 typedef 两个版本的迭代器。
3.2.1 修改一下insert
首先,用过map和set中的insert的朋友,应该知道 insert的返回类型是一个 pair<>,我之前的博客也有详细讲过,所以我们的insert也不例外,返回类型 pair<iterator,bool> 。
然后需要改动的地方就是 之前插入都是直接进行比较的那种,但是 set和map 的比较方式是不一样的,set是用 key直接比,map是用 pair<first,second>中的first来比,所以需要利用第三个模板仿函数来取中要比较的值。
定义一个 仿函数对象:

比较的时候:
if (kot(node)> kot(cur->kv_))
else if (kot(node) < kot(cur->kv_))
最后我们控制一下返回值:
- 在空树里面插入:
return std::make_pair(iterator(_root),true); - 插入相同key的节点
return std::make_pair(iterator(cur), false);
-插入成功
return std::make_pair(iterator(newnode),true);
std::pair<iterator,bool> insert(const T& node)
{
if (_root == nullptr)
{
_root = new Node(node);
_root->col_ = Black;
return std::make_pair(iterator(_root),true);
}
keyofT kot;
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (kot(node)> kot(cur->kv_))
{
parent = cur;
cur = cur->right_;
}
else if (kot(node) < kot(cur->kv_))
{
parent = cur;
cur = cur->left_;
}
else
{
return std::make_pair(iterator(cur), false);
}
}
cur = new Node(node);
Node* newnode = cur;
if (kot(parent->kv_) > kot(cur->kv_))
{
parent->left_ = cur;
cur->parents_ = parent;
}
else
{
parent->right_ = cur;
cur->parents_ = parent;
}
while (parent && parent->col_ == Red)
{
Node* grand = parent->parents_;
/// 插入到左树
if (parent == grand->left_)
{
Node* uncle = grand->right_;
/// 情况一
if (uncle && uncle->col_ == Red)
{
parent->col_ = Black;
uncle->col_ = Black;
grand->col_ = Red;
/// 往上更新
cur = grand;
parent = cur->parents_;
}
/// 情况二 或情况三
else
{
右单旋
if (cur == parent->left_)
{
revolov_R(grand);
parent->col_ = Black;
grand->col_ = Red;
}
else
{
revolov_L(parent);
revolov_R(grand);
cur->col_ = Black;
grand->col_ = Red;
}
break;
}
}
/// 插入到右树
else
{
Node* uncle = grand->left_;
/// 情况一
if (uncle && uncle->col_ == Red)
{
parent->col_ = Black;
uncle->col_ = Black;
grand->col_ = Red;
/// 往上更新
cur = grand;
parent = cur->parents_;
}
else
{
左单旋
if (cur == parent->right_)
{
revolov_L(grand);
parent->col_ = Black;
grand->col_ = Red;
}
else
{
revolov_R(parent);
revolov_L(grand);
cur->col_ = Black;
grand->col_ = Red;
}
break;
}
}
}
_root->col_ = Black;
return std::make_pair(iterator(newnode),true);
}
3.2.2 迭代器的 begin(),end()
这里的begin(),就是中序遍历红黑树的第一个节点,也就是最左节点。
end(),给空的迭代器就好了。
iterator begin()
{
Node* cur = _root;
while(cur && cur->left_)
{
cur = cur->left_;
}
return iterator(cur);
}
iterator end()
{
return iterator(nullptr);
}
3.2.3 修改一下find函数,返回迭代器
iterator find(const K& key)
{
Node* cur = _root;
keyofT kot;
while (cur)
{
if (key > kot(cur->kv_))
{
cur = cur->right_;
}
else if (key > kot(cur->kv_))
{
cur = cur->left_;
}
else
{
return iterator(cur);
}
}
return end();
}
这个简单的很,玩的写。
4. 红黑树继续完善
4.1 红黑树的拷贝构造和赋值重载
默认情况下,是浅拷贝,这完全不能用于 封装map和set,会出大问题。所以需要我们自己来写 。
RBtree(const RBtree<K,T,keyofT>& n)
{
_root = copy(n._root);
}
RBtree<K,T,keyofT>& operator = (RBtree<K,T,keyofT> n)
{
std::swap(_root,n._root);
return *this;
}
Node* copy(Node* root)
{
if (root == nullptr)
{
return nullptr;
}
Node* newnode = new Node(root->kv_);
newnode->col_ = root->col_;
newnode->left_ = copy(root->left_);
newnode->right_ = copy(root->right_);
if (newnode->left_)
{
newnode->left_->parents_ = newnode;
}
if (newnode->right_)
{
newnode->right_->parents_ = newnode;
}
return newnode;
}
这里最关键的是理解 copy函数,用递归完成的。
走的是一个前序,如果root为空,就返回。不为空就以root的数据构造一个新的节点,这里就是深拷贝,然后 它的左树深拷贝root的左树,它的右树深拷贝root的右树。但是 有个问题:红黑树是一个三叉链,它的父子关系也需要维护,怎么才能链接上父亲呢?
它递归结束 返回的上一层的newnode 就是它的父亲,这里还得判断 是否为空。
画个图:
假如我要拷贝上面那颗树:
- 先是深拷贝根节点

- 递归深拷贝它的左子树
- 继续往下递归左子树,其左子树为空,然后返回空。然后递归右子树发现也为空,返回空
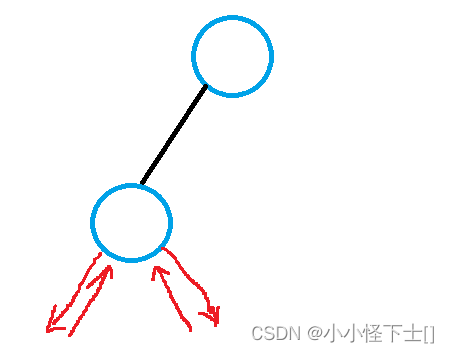
- 然后检测其左右子树返回都是空,所以不需要维护父子关系,直接返回 这个节点
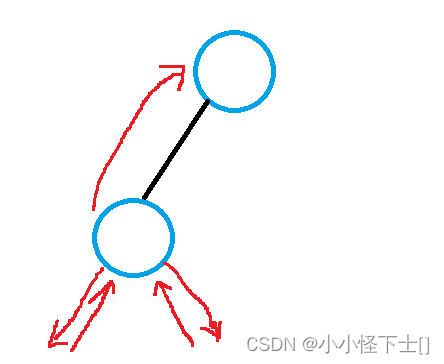
现在就返回到上一层了。
- 递归这一层的右子树,和上面情况一样
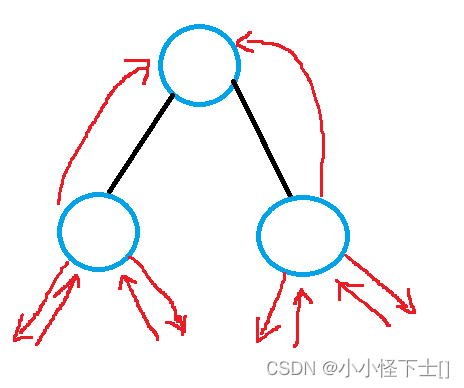
- 检查这一层的左子树和右子树,发现不为空,所以 管理父子关系。
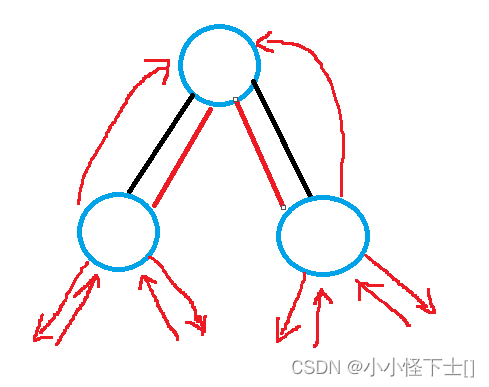
也就是:
newnode->left_->parents_ = newnode;
newnode->right_->parents_ = newnode;
拷贝构造的话,直接调用 copy传入根就好了。
赋值重载的话,这里是有细节的,它是通过传参,这是形参的拷贝构造,然后交换一下 形参的root_ ,就完成了赋值,并且 出了函数调用结束后,它会释放形参,此时的形参中的数据是交换后的数据。
4.2 红黑树的析构函数
红黑树的析构,直接释放掉根节点 行吗?答案是不行,必须递归着 把所有节点都释放掉才可以。
void destroy(Node* root)
{
if (root == nullptr)
{
return ;
}
destroy(root->left_);
destroy(root->right_);
delete root;
}
~RBtree()
{
destroy(_root);
_root = nullptr;
}
上面的递归删除,是一个后序。当然必须是后序。这个大家自行体会吧。
5. 封装红黑树的map和set
其实上文很重要,map和set的底层是红黑树,所以我们必须完善红黑树才能够支持map和set的一些操作。比如 迭代器,拷贝构造,赋值重载,析构等
就相当于 map和set的find,insert,迭代器都是对红黑树中的复用,下面就能很清楚的感觉到了。
5.1 map的模拟实现
template<class K,class V>
class map
{
public:
struct mapkofT
{
const K& operator()(const std::pair<K, V>& t)
{
return t.first;
}
};
typedef typename RBtree<K, std::pair<K, V>, mapkofT>::iterator iterator;
iterator begin()
{
return t_.begin();
}
iterator end()
{
return t_.end();
}
std::pair<iterator,bool> insert(const std::pair<K,V> &i)
{
return t_.insert(i);
}
iterator find(const K& key)
{
return t_.find(key);
}
V& operator[](const K& key)
{
auto i = t_.insert(std::make_pair(key, V()));
return i.first->second;
}
private:
RBtree<K, std::pair<K, V>,mapkofT> t_;
};
对吧,真的比较简单,但是上面还有细节:
typedef typename RBtree<K, std::pair<K, V>, mapkofT>::iterator

必须加上 typename 否则就会报个错误:iterator 依赖名称不是类型。
这个报错说实话,开始我也一头雾水:

它的意思就是 不认为 RBtree<K, std::pair<K, V>, mapkofT>::iterator 是个类型,主要是为什么呢?还没来得及实例化,所以它不是个类型,必须得等到 实例化成功后,它才能算为类型。所以呢 加上个 typename ,告诉编译器,它是一个类型,先让我编译通过。

还有个[]的实现,我之前写了一篇博客,里面很详细的介绍了这个,但是 没有讲实现,现在模拟实现了一下,发现不是想象中的那么高级:
调用了insert,利用了它的返回值
V& operator[](const K& key)
{
auto i = t_.insert(std::make_pair(key, V()));
return i.first->second;
}
5.2 set的模拟实现
template<class K>
class set
{
public:
struct setketofT
{
const K& operator()(const K& k)
{
return k;
}
};
typedef typename RBtree<K, K, setketofT>::iterator itetator;
// 迭代器
itetator begin()
{
return t_.begin();
}
itetator end()
{
return t_.end();
}
std::pair<itetator, bool> insert(const K& key)
{
return t_.insert(key);
}
itetator find(const K& key)
{
return t_.find(key);
}
private:
RBtree<K,K,setketofT> t_;
};
6. 总结
有问题的私信,或评论。感觉有帮助的朋友,可以点一个小赞,支持一下。
