当前位置：首页 > news >正文

LeetCode·每日一题·940.不同的子序列 || · 动态规划

news 来源：原创 2024/9/9 3:51:32

链接：https://leetcode.cn/problems/distinct-subsequences-ii/solutions/1891268/di-gui-hui-su-dong-tai-gui-hua-zhu-shi-c-m6ac/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处

题目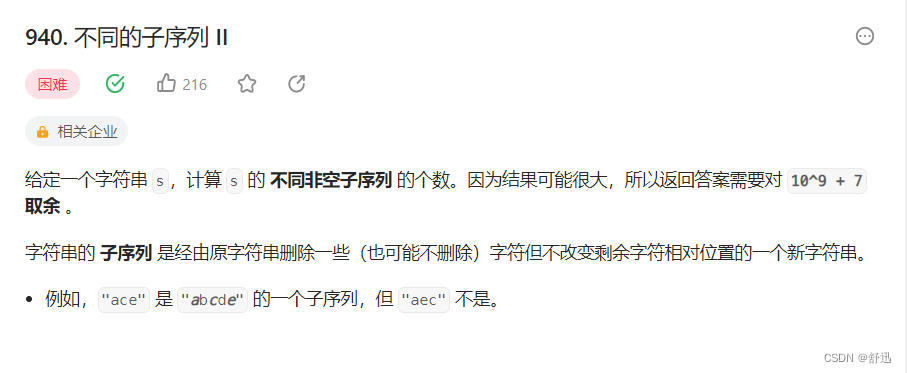

示例

思路

题意 -> 给定一个字符串 s，计算 s 的不同非空子序列的个数

C语言库函数实现哈希表，力扣也支持

【递归+回溯】

根据题目意思直接枚举 s 中所有非空子序列，最后统计总数即可

当然我们枚举所有的子序列，肯定是会存在重复子序列的，对于重复的子序列我们只能进行一次统计，所以使用哈希表对子序列进行去重，每次枚举出一个子序列就判断是否在哈希表中存在

递归枚举的过程我们可以不全部枚举出去，对于一些明显重复的子序列我们可以直接不枚举，并利用回溯返回上一步

具体看代码，注释超级详细

当然递归过不了！！！！

【动态规划】

动态规划思路不太好想

对于 s 中任意一个字符，当我们选择这个字符并构造当前字符的子序列时，存在两种构造方法：

当前字符为结尾：需要选择当前字符的前一个元素
- 对应的 dp[i] 表示为以字符 i 结尾的子序列有多少个
  - 递推公式：dp[i] = dp[i-1] + 1;
    - 遍历方向：因为当前位置需要前一个才能推出，所以要从前往后枚举
当前字符为开头：需要选择当前字符的后一个元素
- 对应的 dp[i] 表示为以字符 i 开始的子序列有多少个
  - 递推公式：dp[i] = dp[i+1] + 1;
    - 遍历方向：因为当前位置需要后一个才能推出，所以要从后往前枚举

初始化都为 1，因为一个字符就是一个子序列

这两种方法都可以进行构造，只是在遍历方向上面不一样

到这里其实我们已经实现了所以非空子序列的枚举，但是我们没有去重，在这里dp中存在很多重复的子序列，那么对于去重我们还是的用哈希表，这里就可以用数组哈希来进行简单去重了。

去重

对于上述dp中当我们确定一个元素时，都存在下一个元素或者上一个元素的选择

比如 baaabaabcc，当我们选择了第三个 a 时，也就是确定了 dp[i],接下来就是dp[i+1]的选择，当然最简单就是枚举之后的每一个元素，但是就会存在重复的子序列，比如选择了第二个 a 相加之后，再选择第一个 a 相加，其实在第二个 a中就已经包含了选择第一个a相加的情况，就会重复。所以可以使用数组哈希记录相同元素最后出现的位置，每次选择下一个元素时，只从数组哈希中选择

从dp数组的含义理解：对于上一个元素也还是以字符 i 结尾的子序列有多少个，那么字符只有26个，所以选择上一个结尾字符时也肯定只有26个选择

1 e 9 + 7 是科学计数法 = 1 * 10^9 + 7

代码

【递归+回溯】

//哈希+递归+回溯
struct my_struct {
    char name[2000];          /* key */
    int id;
    UT_hash_handle hh;         /* makes this structure hashable */
};
struct my_struct * users = NULL;

void dfs(char * s, int len, int index, char * path, int next, int * count)
{
    struct my_struct * m = NULL;
    if(index == len)    return;
    int mod = 1e9 + 7;
    for(int i = index; i < len; i++)//枚举切割点
    {
        path[next] = s[i];
        HASH_FIND_STR(users, path, m);
        if(!m)//只有不存在时才切割
        {
            m = (struct my_struct *)malloc(sizeof *m);
            strcpy(m->name, path);
            m->id = i;
            HASH_ADD_STR(users, name, m);
            (*count)++;
            (*count) %= mod;
            dfs(s, len, i+1, path, next+1, count);//下一个切割点
        }
        path[next] = '\0';//回溯
    }
}

int distinctSubseqII(char * s){
    int len = strlen(s);
    char path[len+1];
    memset(path, 0, sizeof(path));
    int count = 0;
    struct my_struct *m, *tmp = NULL;
    dfs(s, len, 0, path, 0, &count);

    /* free the hash table contents */
    HASH_ITER(hh, users, m, tmp) {
      HASH_DEL(users, m);
      free(m);
    }
    return count;
}

作者：小迅要变强
链接：https://leetcode.cn/problems/distinct-subsequences-ii/solutions/1891268/di-gui-hui-su-dong-tai-gui-hua-zhu-shi-c-m6ac/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

【动态规划】

int distinctSubseqII(char * s){
    int hash[26];
    memset(hash, -1, sizeof(hash));
    int len = strlen(s);
    int dp[len];
    int mod = 1e9 + 7;//初始化
    for(int i = 0; i < len; ++i)//枚举数组
    {
        dp[i] = 1;//初始化为 1，
        for(int j = 0; j < 26; j++)//枚举数组
        {
            if(hash[j] != -1)//选择上一个结尾元素
            {
                dp[i] = (dp[i] + dp[hash[j]]) % mod;
            }
        }
        hash[s[i] - 'a'] = i;
    }
    int count = 0;
    for(int i = 0; i < 26; i++)//统计所以字符结尾的子序列，总共只有26个字符
    {
        if(hash[i] != -1)
            count = (count + dp[hash[i]]) % mod;
    }
    return count;
}

作者：小迅要变强
链接：https://leetcode.cn/problems/distinct-subsequences-ii/solutions/1891268/di-gui-hui-su-dong-tai-gui-hua-zhu-shi-c-m6ac/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。